CONVEXITÉ - Ensembles convexes

CONVEXITÉ - Ensembles convexes

Un sous-ensemble C d’un espace vectoriel réel E est dit convexe si, pour tout couple de points quelconques de C, le segment qui a pour extrémités ces deux points est entièrement contenu dans C. Par exemple, un cube est convexe, mais sa surface ne l’est pas, car elle ne contient le segment d’extrémités x et y que si x et y appartiennent à la même face. Les ensembles convexes interviennent dans de nombreux domaines des mathématiques et il est souvent possible, en pareil cas, d’obtenir d’intéressants résultats en ne faisant appel qu’à des arguments «géométriques» relativement élémentaires.

Minkowski (1864-1909) fut le premier à étudier systématiquement les ensembles convexes et ses œuvres contiennent la plupart des idées importantes utilisées pour ce sujet. Les premiers développements se limitaient aux espaces vectoriels de dimension finie et l’objet principal de ces études était de résoudre des problèmes de nature quantitative; depuis 1940, les aspects combinatoires et qualitatifs ont bénéficié d’une plus grande attention. Après quelques préliminaires généraux, on traitera d’abord les aspects quantitatifs et combinatoires, en se limitant au cas où l’espace est de dimension finie; on abordera ensuite les aspects qualitatifs de la théorie et ses applications à l’analyse fonctionnelle.

Un des aspects les plus fascinants de la théorie des ensembles convexes est le grand nombre de problèmes très faciles et intuitifs à formuler que l’on ne sait pas toujours résoudre.

1. Propriétés générales

Définitions

Soit x et y , deux points distincts d’un espace vectoriel réel E (cf. algèbre LINÉAIRE ET MULTILINÉAIRE). Par analogie avec le cas de l’espace usuel R³ (représentation paramétrique de la droite définie par deux points), on appelle droite joignant x et y l’ensemble des points de E de la forme:

où est un nombre réel quelconque. Les points tels que 閭 0 constituent la demi-droite xy d’origine x ; les points tels que 0 諒 諒 1 constituent le segment [x , y ] d’extrémités x et y.

Par définition, on appelle sous-variété linéaire de E tout sous-ensemble de E qui contient toute droite joignant deux quelconques de ses points; par exemple, dans l’espace usuel R³, les sous-variétés linéaires sont: l’ensemble vide, les ensembles réduits à un point, les droites, les plans et l’espace R³ tout entier. Toute sous-variété linéaire V de E est la translatée d’un sous-espace vectoriel de E, c’est-à-dire l’ensemble des points de la forme a + x , où a est un élément fixé de V et où x parcourt un sous-espace vectoriel F de E; si F est de dimension finie p , on dit que V est de dimension p.

Par analogie avec le cas des plans dans R³, on appelle hyperplan de E toute sous-variété linéaire qui n’est contenue strictement dans aucune autre variété linéaire que E lui-même; par exemple, les hyperplans de Rⁿ sont les variétés linéaires de dimension n 漣 1. Le complémentaire (ensembliste) d’un hyperplan H est la réunion (ensembliste) de deux ensembles convexes disjoints appelés les demi-espaces ouverts limités par H; leurs réunions avec H s’appellent les demi-espaces fermés limités par H. On dit que deux ensembles X et Y sont séparés par H si l’un est contenu dans un de ces deux demi-espaces fermés et l’autre dans l’autre demi-espace; on dit que H est un hyperplan d’appui de X au point x si x appartient à X et si X et x sont séparés par H. La figure 1 donne un exemple d’un hyperplan H d’appui de X en x , séparant X et Y (ici E = R², et H est une droite).

Ensembles convexes

Un sous-ensemble C de E est dit convexe si pour tout couple x , y de points distincts de C, le segment [x , y ] est entièrement contenu dans C (fig. 2). Il est clair que toute intersection d’ensembles convexes est encore un ensemble convexe. Par suite, si X est un sous-ensemble quelconque de E, l’intersection お de tous les ensembles convexes contenant X (il y en a toujours au moins un, E lui-même) est un ensemble convexe contenant X qui possède la propriété d’être contenu dans tout ensemble convexe contenant X; お s’appelle l’enveloppe convexe de X (fig. 3). On peut aussi définir X comme l’ensemble de toutes les combinaisons convexes des points de X, c’est-à-dire l’ensemble des points de la forme:

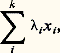où les x ⁱ sont des points de X et où lesⁱ sont des nombres réels positifs quelconques de somme 1. On appelle enveloppe convexe fermée de X l’adhérence de お.

Les enveloppes convexes des sous-ensembles finis de Rⁿ sont appelées des polytopes (cf. infra ). En particulier, on appelle simplexe de dimension n l’enveloppe convexe de (n + 1) points distincts de Rⁿ non situés dans un même hyperplan (segment pour n = 1, triangle pour n = 2, tétraèdre pour n = 3, etc.); cette notion joue un rôle fondamental en topologie algébrique.

Un point x d’un ensemble convexe C est appelé un point extrémal si son complémentaire dans C est convexe, c’est-à-dire si x n’appartient à l’intérieur d’aucun segment contenu dans C. Une face F de C est un sous-ensemble convexe de C tel qu’aucun segment contenu dans C ne traverse F, c’est-à-dire que tout segment [x , y ] dont les extrémités appartiennent à C et dont un point différent des extrémités appartient à F est entièrement contenu dans F. Ainsi, le cube a six 2-faces, douze 1-faces (les arêtes) et huit 0-faces (les sommets); de plus, le cube est l’enveloppe convexe de ses points extrémaux, qui sont ici les sommets.

Les termes corps et cônes sont utilisés de manière assez différente par plusieurs auteurs. Nous adopterons les définitions suivantes: Un corps est un sous-ensemble borné de Rⁿ d’intérieur non vide (c’est-à-dire contenant au moins une boule de rayon 礪 0) et un cône est un sous-ensemble d’un espace vectoriel réel E, qui est réunion d’une famille de demi-droites de même origine.

2. Aspects quantitatifs

Géométrie des nombres

Ce sont des recherches de théorie des nombres qui furent à l’origine des premiers travaux de Minkowski. Nous renvoyons, pour cet aspect, à l’article approximations DIOPHANTIENNES, en nous contentant de rappeler ici l’énoncé du célèbre théorème de Minkowski: Si C est un sous-ensemble convexe de Rⁿ , symétrique par rapport à l’origine, et de volume V(C) 閭 2ⁿ , alors C contient au moins un point dont toutes les coordonnées sont des nombres entiers.

Empilements

Un empilement est un arrangement de corps convexes tel qu’aucune paire de ces corps n’ait de point intérieur en commun. Indépendamment de l’intérêt que les problèmes d’empilements ont en eux-mêmes, ce genre de problèmes se retrouve également en théorie des nombres, en théorie de l’information, en cristallographie, en botanique, en construction des réacteurs nucléaires, etc. Très souvent, on cherche à réaliser un empilement de densité maximum. Ainsi, l’empilement de densité maximum de cercles égaux dans le plan est obtenu en décomposant le plan en hexagones réguliers égaux et en inscrivant dans chacun de ces hexagones le cercle de diamètre maximum; ainsi, chaque cercle en touche exactement six autres (fig. 4). Dans le cas de l’espace à trois dimensions, on a conjecturé que l’empilement de densité maximum de boules égales est obtenu par une construction due à Kepler: on commence par diviser R³ en un échiquier à trois dimensions, où les cubes sont coloriés alternativement en blanc et en noir; on construit ensuite des boules centrées en chacun des centres des cubes noirs et tangentes à chacune des douze arêtes du cube; de cette façon, chacune des boules en touche exactement douze autres. Cette conjecture n’a été démontrée que pour des empilements assez réguliers.

Inégalités

Il y a toute une série de résultats quantitatifs relatifs au volume, à la surface, au diamètre, etc., d’un corps convexe. Par exemple, l’inégalité isopérimétrique exprime que la surface S et le volume V d’un corps convexe C de Rⁿ vérifient l’inégalité:

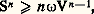où 諸 est le volume de la boule unité de Rⁿ ; de plus, cette inégalité est une égalité si et seulement si C est une boule, c’est-à-dire que, parmi les corps convexes de volume donné, les boules constituent ceux dont la surface est minimum. De plus, tout corps convexe C de Rⁿ est contenu dans une boule de rayon minimum r , et cette boule est unique; l’inégalité de Jung affirme que si on désigne par d le diamètre du corps C (c’est la borne supérieure des longueurs des segments dont les extrémités appartiennent à C), on a:

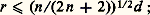cette inégalité devient une égalité si et seulement si C est un simplexe régulier de n + 1 sommets dans Rⁿ . Un théorème de Loewner affirme que tout corps de Rⁿ est contenu dans un ellipsoïde de volume minimum; cet ellipsoïde joue un rôle important dans la théorie des modèles expérimentaux.

Volumes mixtes

Soit C¹, C², ..., C^k des corps convexes de Rⁿ , et¹,², ...,^k des nombres réels positifs; l’ensemble des points de la forme: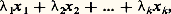

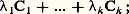où x ⁱ parcourt Cⁱ pour tout i , est un corps convexe C, que nous désignerons par:

lorsque C¹, ..., C^k sont fixés, le volume de C s’exprime par un polynôme homogène de degré n en les variables¹, ...,^k . Certains des problèmes les plus fondamentaux de la théorie quantitative des corps convexes sont liés à l’étude des coefficients de ces polynômes, appelés volumes mixtes de C¹, ..., C^k . L’outil de base, dans l’étude des volumes mixtes, est le théorème de Brunn-Minkowski, qui affirme que, pour tout compris entre 0 et 1, on a:

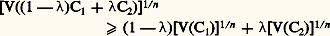c’est-à-dire que la racine n -ième du volume est une fonction concave de. Les inégalités pour les volumes mixtes engendrent de nombreuses inégalités d’intérêt géométrique, en particulier l’inégalité isopérimétrique.

Corps de largeur constante

Un corps convexe C de Rⁿ est dit de largeur constante b si la distance entre n’importe quelle paire d’hyperplans d’appui de C parallèle est constante, égale à b. Contrairement à l’intuition, un tel corps n’est pas nécessairement circulaire (dans le plan) ou sphérique. La définition précédente équivaut à la suivante: C a pour diamètre b et tout ensemble réunion de C et d’un point quelconque de Rⁿ n’appartenant pas à C est de diamètre supérieur à b. Par suite, tout ensemble de Rⁿ de diamètre 諒 b est contenu dans un corps convexe de largeur constante b. Cette propriété permet, par exemple, de ramener le problème suivant de Borsuk au cas où X est de largeur constante: Peut-on recouvrir tout ensemble X de diamètre 1 de Rⁿ par (n + 1) ensembles de diamètres 麗 1? La réponse est affirmative si n 諒 3, mais inconnue pour n 礪 3.

Euler (en 1778) et de nombreux mathématiciens après lui ont étudié les corps convexes de largeur constante dans le plan (n = 2); les propriétés trouvées ont été utilisées en cinématique et même pour construire un foret utilisé pour forer des trous carrés: un corps possédant ces propriétés peut être placé dans un carré de telle sorte qu’en les tournant il reste perpétuellement en contact avec les quatre côtés de la boîte.

3. Aspects combinatoires

Intersections

Une partie des problèmes combinatoires est reliée à l’étude des intersections d’ensembles convexes qui sont toujours convexes, comme on l’a vu ci-dessus (l’ensemble vide est, par définition, convexe).

D’après un théorème démontré par Helly, l’intersection C d’une famille de convexes de Rⁿ , telle que l’intersection de toute sous-famille de (n + 1) de ces ensembles soit non vide, est non vide si l’une ou l’autre des hypothèses suivantes est réalisée: la famille est finie ou chacun des convexes de la famille est fermé et borné (c’est-à-dire compact). Ce théorème admet de nombreuses généralisations et applications.

L’étude des propriétés des intersections d’ensembles convexes est facilitée par la notion de graphe d’intersection, qui est utilisée dans des domaines aussi variés que la génétique moléculaire, la psychologie et l’écologie. Pour toute famille d’ensembles, on appelle graphe d’intersection un graphe abstrait où chaque ensemble correspond à un sommet du graphe et où chaque intersection non vide est représentée par un arc réunissant les sommets correspondants; la figure 5 donne un exemple d’une famille d’ensembles convexes et de leur graphe d’intersection. Tout graphe ayant un nombre fini d’éléments est un graphe d’intersection d’ensembles convexes de R³, mais pas nécessairement un graphe d’intersection d’ensembles convexes de R² ou de R. Un graphe d’intervalles est un graphe d’intersection d’une famille finie d’ensembles convexes de R (ce sont des intervalles); on peut caractériser ces graphes d’intervalles, mais le problème correspondant pour le plan n’est pas résolu.

Étude des enveloppes convexes

Une autre série de problèmes combinatoires est la recherche de formes algébriques pour la représentation des enveloppes convexes. Voici, dans cet ordre d’idées, un théorème très simple et très utile, dû à Carathéodory: Si X est un sous-ensemble de Rⁿ et u un point de l’enveloppe convexe de X, alors u appartient à l’enveloppe convexe d’un sous-ensemble fini Y de X contenant au plus (n + 1) points. Par exemple, si X est un sous-ensemble du plan et si x appartient à l’enveloppe convexe de X, alors x appartient soit à X, soit à un segment ayant pour extrémités deux points de X, soit à un triangle ayant pour sommet trois points de X. Le théorème de Carathéodory a de nombreuses applications; on en déduit, par exemple, que l’enveloppe convexe d’un ensemble fermé borné de Rⁿ est un ensemble fermé borné.

Polyèdres

Parmi tous les problèmes combinatoires que l’on rencontre dans la théorie de la convexité, celui qui est le plus ancien et qui a été étudié de la manière la plus approfondie est la structure des faces des polyèdres convexes. Nous appellerons polyèdre tout sous-ensemble de Rⁿ intersection d’un nombre fini de demi-espaces fermés, en réservant la dénomination de polytope , aux polyèdres bornés ; un lemme, dû à Farkas, montre qu’un ensemble est un polytope si et seulement s’il est l’enveloppe convexe d’un nombre fini de points. On peut caractériser de même les cônes polyédraux comme enveloppes convexes d’un nombre fini de demi-droites de même origine. De manière générale, un sous-ensemble P de Rⁿ est un polyèdre si et seulement s’il satisfait à une des conditions équivalentes suivantes:

a ) P est un ensemble convexe fermé qui a un nombre fini de faces;

b ) P est l’enveloppe d’un nombre fini de points et de demi-droites;

c ) P est la somme vectorielle B + C d’un polytope B et d’un cône polyédral C, c’est-à-dire P est l’ensemble des points de la forme:

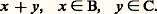d ) P est l’enveloppe convexe fermée de la réunion d’un polytope B et du translaté d’un cône polyédral. (On a représenté, sur la figure 6, un polyèdre P de dimension 2, ainsi que le polytope B et le cône C mentionnés ci-dessus.)

Le premier résultat, dans l’étude combinatoire des polytopes est le théorème d’Euler (1752), qui affirme que si v , e , f sont respectivement le nombre de sommets, d’arêtes et de faces d’un polytope de dimension 3 , on a:

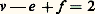(on appelle ici sommets les points extrémaux du polyèdre). Poincaré et Schläfli ont généralisé ce théorème aux polytopes de dimension n : si f ⁱ (P) est le nombre de faces de P de dimensions i , on a la relation:

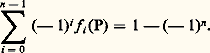En 1934, Steinitz est parvenu à caractériser les graphes des polytopes de dimension 3 (on appelle graphe d’un polytope la structure combinatoire déterminée par les sommets et les arêtes): le graphe d’un polytope de dimension 3 est équivalent à un graphe planaire (qui peut se dessiner dans le plan sans qu’il y ait aucune intersection d’arcs) connexe de degré 3 (c’est-à-dire qui ne peut être séparé en deux parties disjointes en enlevant moins de trois sommets). Par exemple, le graphe de la figure 7 est le graphe du polytope obtenu en tronquant chacun des sommets d’un cube; les deux graphes de la figure 8 ne sont pas des graphes de polytopes de dimension 3, car le premier n’est pas connexe de degré 3 et le second n’est pas semblable à un graphe planaire (c’est le graphe d’un simplexe de dimension 4). On a découvert de nombreuses propriétés des graphes des polytopes de dimension n (par exemple, ils sont connexes de degré n ), mais on ne connaît à ce jour aucune caractérisation combinatoire des graphes des polytopes de dimension 礪 3.

De nombreux problèmes de programmation linéaire et d’optimisation ^{[cf. OPTIMISATION ET CONTRÔLE]} reviennent à trouver les points d’un polyèdre P où une fonction linéaire atteint son minimum; on montre que, si P est borné, le minimum est alors atteint en un des sommets de P et certains procédés de résolution de programmes linéaires reposent sur cette propriété. On est donc amené à estimer le nombre de sommets d’un polytope P en fonction de sa dimension et du nombre de faces de dimension (n 漣 1). Pour 2 諒 n 麗 k , désignons par 猪(n , k ) le nombre maximum de sommets que possède un polyèdre de dimension n qui a k faces de dimension (n 漣 1) et par 﨏(n , k ) la somme des coefficients binomiaux:

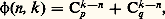pour p = k 漣 [(n +1)/2], q = k 漣 [(n + 2)/2], en désignant par [r ] la partie entière de r , c’est-à-dire le plus grand entier 諒 r ; avec ces notations, on a alors:

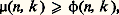et cette inégalité devient en fait une égalité si n 諒 8, ou k 諒 n + 3, ou k 閭 n ²/4 (on ne sait s’il y a toujours égalité). L’étude de la fonction 猪 montre, par exemple, le fait remarquable que pour tout k 礪 n , il y a un polytope de dimension n à k sommets tel que chaque groupe de [n /2] sommets détermine une face: ainsi, il y a des polytopes de dimension 4 avec un nombre quelconque de sommets où chaque paire de sommets est reliée par une arête du polytope.

4. Aspects qualitatifs

Contrairement à ce qui précède, les espaces considérés ici sont quelconques, et non nécessairement de dimension finie.

La convexité intervient de manière essentielle dans les espaces vectoriels de l’analyse: espaces vectoriels normés, ou plus généralement espaces vectoriels topologiques localement convexes, c’est-à-dire où tout point a un système fondamental de voisinages convexes; on se limitera ici à de rapides indications, en renvoyant pour les définitions aux articles espaces vectoriels NORMÉS et espaces vectoriels TOPOLOGIQUES.

Espaces normés

On soulignera seulement le rôle de la convexité. Rappelons qu’une norme sur un espace vectoriel E (qui sera ici réel) est une fonction p à valeurs positives définie dans E telle que:

a ) p (x ) = 0 si et seulement si x = 0;

b ) p (x ) = || p (x ) pour x 捻 E et 捻 R;

c ) p (x + y ) 諒 p (x ) + p (y ) (sous-additivité).

Une norme est souvent notée 瑩. 瑩.

L’étude des espaces vectoriels normés est, d’une certaine façon, l’équivalent de l’étude d’une classe d’ensembles convexes; le lien est établi par la fonction de jauge. Si 瑩. 瑩 est une norme sur E, on appelle boule unité (resp. sphère unité ) pour cette norme l’ensemble des x 捻 E tels que 瑩x 瑩 諒 (resp. 瑩x 瑩 = 1). Les propriétés de la norme entraînent que la boule unité U est un ensemble convexe dont l’intersection avec toute droite passant par O est un segment symétrique [ 漣 x , x ] (non réduit au point O). Réciproquement, soit U un ensemble convexe satisfaisant à ces propriétés; pour tout x 0, désignons par p (x ) le plus petit entier positif tel que x / 捻 U et posons p (0) = 0 (la fonction p est appelée la jauge de l’ensemble U). On vérifie facilement que la jauge de U est une norme sur E pour laquelle U est la boule unité (en fait, la jauge d’un ensemble peut se définir sous des hypothèses beaucoup plus générales). Ainsi toutes les propriétés d’un espace normé peuvent être décrites uniquement en fonction de sa boule ou de sa sphère unité. Par exemple, la convexité stricte d’un espace vectoriel normé, caractérisée par l’inégalité stricte 瑩x + y 瑩 麗 瑩x 瑩 + 瑩y 瑩 lorsque x et y ne sont pas sur une même demi-droite d’origine O, équivaut au fait que sa sphère unité ne contient aucun segment.

On appelle espace de Minkowski tout espace vectoriel normé de dimension finie. Par exemple, pour tout r 閭 1:

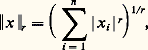où x = (x ¹, ..., x ⁿ ) 捻 Rⁿ , est une norme sur Rⁿ ; pour r = 2, on retrouve la norme euclidienne usuelle. Une autre norme importante sur Rⁿ est la norme:

x = (x ¹, ..., x ⁿ ) 捻 Rⁿ , pour laquelle la boule unité est l’hypercube de Rⁿ .

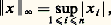Tous les problèmes quantitatifs indiqués ci-dessus ont fait l’objet d’études analogues pour les espaces de Minkowski: inégalité isopérimétrique, inégalité de Jung, etc.

Théorèmes de séparation

En analyse fonctionnelle, en théorie des jeux, en intégration et même dans certains problèmes relatifs aux graphes coloriés en théorie des graphes, on utilise des théorèmes de séparation et de support.

Les théorèmes de séparation établissent les conditions sous lesquelles on peut séparer (au sens du chapitre 1) deux sous-ensembles convexes disjoints X et Y d’un espace vectoriel topologique E. Pour que cela soit possible, il suffit, par exemple, que l’une des conditions suivantes soit réalisée:

a ) E est de dimension finie;

b ) un des deux ensembles a un intérieur non vide;

c ) un des deux ensembles est fermé, l’autre compact, et E est localement convexe.

Dans chacun de ces cas, on peut choisir l’hyperplan de séparation fermé, c’est-à-dire défini comme l’ensemble des zéros d’une fonction affine continue.

Remarquant que l’intérieur d’un ensemble convexe est convexe, on en déduit que si A est un ensemble convexe d’intérieur non vide et A une sous-variété linéaire de E ne rencontrant pas l’intérieur de C, alors il existe un hyperplan qui contient A et qui sépare A de C (forme «géométrique» du théorème de Hahn-Banach). En particulier, si C est un ensemble convexe d’intérieur non vide, C admet un hyperplan d’appui en chaque point de sa frontière (théorème de Mazur). On ne peut pas étendre ce théorème au cas où C n’a pas de point intérieur, mais on peut montrer que, dans certains cas (C fermé dans un espace de Banach, ou C compact pour la topologie faible d’un espace localement convexe), les points de la frontière de C, où C admet un hyperplan d’appui, forment un sous-ensemble dense de la frontière de C.

Soit A une sous-variété linéaire d’un espace vectoriel E, p une fonction convexe dans E (cf. CONVEXITÉ – Fonctions convexes), et f une fonction affine définie dans A telle que f (x ) 諒 p (x ) en tout point x de A; alors il existe une fonction affine g définie dans E qui prolonge f (c’est-à-dire que g (x ) = f (x ) pour tout x 捻 A) telle que l’on ait g (x ) 諒 p (x ) en tout point x 捻 E (théorème de Hahn-Banach). Ce résultat, essentiel en analyse fonctionnelle, équivaut en fait aux théorèmes énoncés ci-dessus: il résulte, par exemple, du théorème de séparation en prenant pour ensembles le graphe de la fonction f et l’épigraphe de la fonction p . D’autre part, ce théorème de Hahn-Banach entraîne que si C est un ensemble convexe contenant l’origine comme point intérieur et si u est un point frontière de C, alors C admet un hyperplan d’appui en u (on retrouve le théorème de Mazur; il faut prendre comme fonction convexe p la jauge de C).

Points extrémaux

Les fonctions convexes et concaves présentent des propriétés très utiles dans les problèmes d’optimisation. Par exemple, soit f une fonction convexe définie dans un domaine convexe D d’un espace vectoriel topologique localement convexe E; alors tout minimum local de f dans D est un minimum global , c’est-à-dire que si un point x ⁰ de D possède un voisinage U tel que f (x ) 閭 f (x ⁰) pour tout x 捻 U 惡 D, alors cette inégalité est valable pour tout x 捻 D. Si f est concave et D compact, alors f atteint son minimum en un point extrémal de D; cette propriété justifie l’étude des points extrémaux en analyse fonctionnelle.

Le théorème de Krein-Milman attire l’attention sur d’autres propriétés importantes des points extrémaux. Ce théorème établit que si C est un sous-ensemble compact convexe d’un espace localement convexe et si X est un sous-ensemble de C, alors C est l’enveloppe convexe fermée de X si et seulement si l’adhérence de X contient tous les points extrémaux de C; ainsi, l’adhérence de l’ensemble des points extrémaux de C est le plus petit sous-ensemble X de C tel que chaque point de C soit adhérent à l’ensemble des combinaisons convexes (cf. chap. 1) de points de X. On peut généraliser ce théorème au cas où C n’est pas compact moyennant des hypothèses supplémentaires; par exemple, si C est un convexe fermé de Rⁿ ne contenant aucune droite, alors C est l’enveloppe convexe de ses points extrémaux et de ses demi-droites extrémales (il n’est pas nécessaire de prendre l’enveloppe convexe fermée; par définition, une demi-droite extrémale de C est une demi-droite qui n’est «traversée» par aucun segment contenu dans C).

Voici une application du théorème de Krein-Milman à l’analyse fonctionnelle. Soit C un sous-ensemble compact convexe d’un espace localement convexe E et soit X l’ensemble de tous les points extrémaux; alors, d’après le théorème de Krein-Milman, pour tout point p de C, il existe une mesure positive 猪 sur l’adhérence 淚 de X telle que 猪(X) = 1 et telle que:

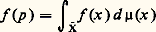pour toute forme linéaire continue f (p ) est le «barycentre» de la mesure 猪). Ce résultat entraîne de nombreux théorèmes de représentation intégrale en analyse.

Théorèmes de point fixe

Indiquons rapidement, pour conclure, deux théorèmes de point fixe pour les ensembles convexes.

Le théorème de Brouwer-Schauder-Tychonov montre que si C est un compact convexe d’un espace localement convexe et f une application continue de C dans lui-même, il existe au moins un point p de C tel que f (p ) = p. Ce théorème permet d’obtenir des théorèmes d’existence pour les solutions des équations différentielles et intégrales, les théorèmes du minimax en théorie des jeux et de nombreuses propriétés des ensembles convexes. Par exemple un compact C de Rⁿ ou d’un espace de Hilbert H est convexe si pour chaque point x de l’espace, il y a un point unique de C qui minimise la distance entre x et C (pour Rⁿ , il suffit que C soit fermé; dans le cas d’un espace de Hilbert quelconque le problème n’est pas résolu).

Le théorème de Markov-Kakutani affirme que si C est un compact convexe d’un espace vectoriel topologique et si 淋 est une famille commutative de transformations affines continues de C dans C, alors il y a au moins un point p de C tel que f (p ) = p pour toute fonction de 淋. Ce théorème sert à établir l’existence de mesures invariantes pour les groupes commutatifs et à construire des mesures qui généralisent la mesure de Lebesgue pour les ensembles bornés de Rⁿ .

Encyclopédie Universelle. 2012.